Для Маши Симоновой
Мама купила Оле, Саше и Паше по — мороженому: пломбир, шоколадное и клубничное. Оля ест не клубничное и не пломбир. Саша не пломбир и не шоколадное, Паша не любит шоколад и клубничное мороженое. Какое мороженое ест каждый ребенок?
Начертим таблицу и заполним ее данными. Чертим таблицу 4х3. Не подходящее по условию значение обозначим <<->> , подходящее <<+>>.

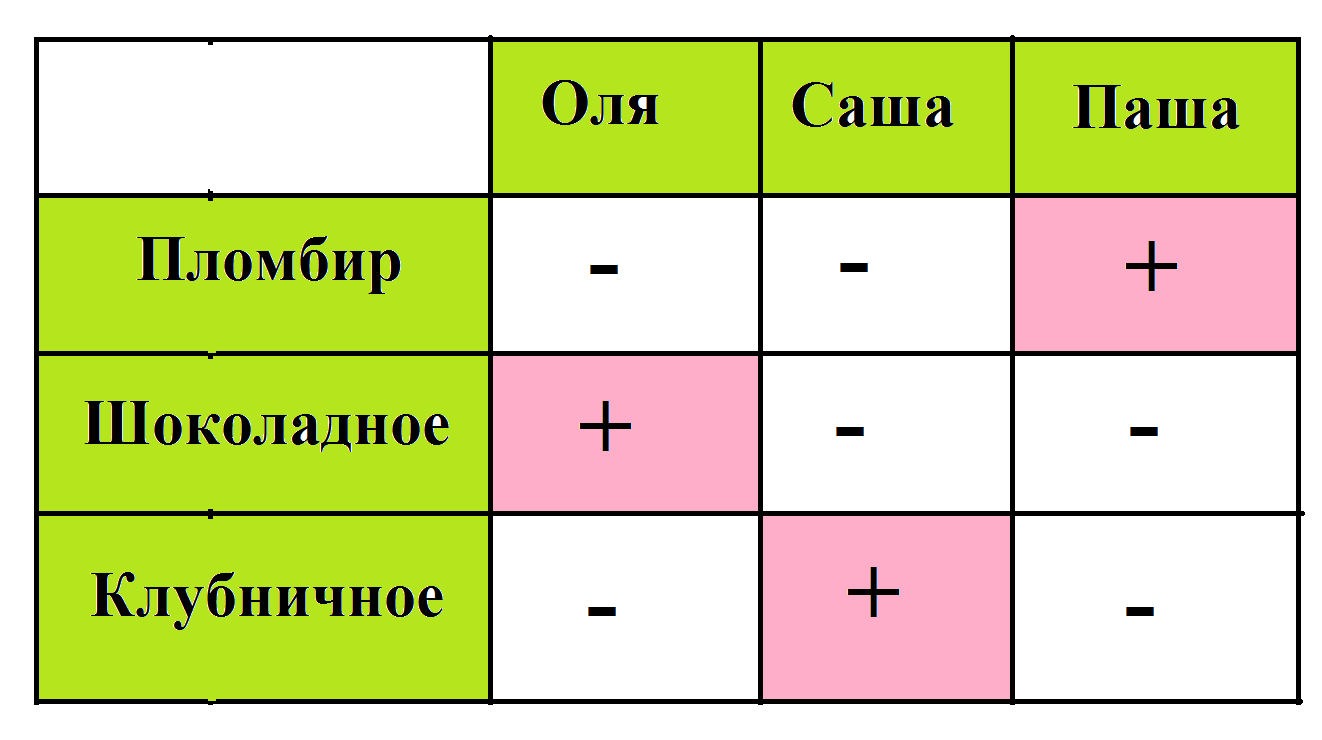
Так как Оля ест не клубничное и не пломбир, в эти графы ставим минус. Получается, что для Оли подходит шоколадное, там ставим плюс. Саша ест не пломбир и не шоколадное, ставим там минус. Для нее подходящее значение клубничное. Так как Паша не любит шоколад, то и мороженное шоколадное он есть не будет, ставим минус, и на клубничное тоже. Паша ест пломбир.
Ответ: Оля-шоколадное, Саша-клубничное, Паша-пломбир.
Текстовые задачи типа <<Считаем ноги и головы>> очень популярны в математических олимпиадах и в заданиях со звездочкой в учебнике.
На ферме живут гуси и овцы. В сумме у них 40 голов и 94 ноги. Сколько на ферме проживает гусей? и сколько овец?


Разберемся для начала со всеми ногами. Мы знаем, что у овцы их четыре, а гуся две. Давайте посчитаем так, если у всех по две ноги. Так как голов 40, то получается:
40 • 2 = 80 ног.
По условию в задаче всего 94 ноги, найдем так называемые <<лишние>> ноги:
94 — 80 = 14.
Если эти 14 ног лишние, значит они принадлежат четвероногим овцам, и теперь мы сможем определить количество овец:
14 : 2 = 7 овец.
Теперь осталось вычислить сколько на ферме гусей. Для этого просто вычтем из общего числа голов те, которые принадлежат овцам:
40 — 7 = 33 гуся.
Ответ: 7 овец и 33 гуся.
Еще одна не менее популярная задача на <<рукопожатия>>.
Ваня на детской площадке встретил своих друзей Петю, Машу и Колю. При встрече они все обменялись рукопожатиями. Сколько всего было рукопожатий при встрече?
 Каждого человека обозначаем точкой. Потом от каждой точки проводим
отрезки к тем, с которыми нужно пожать руки. Считаем количество
отрезков, оно и будет ответом в задаче.
Каждого человека обозначаем точкой. Потом от каждой точки проводим
отрезки к тем, с которыми нужно пожать руки. Считаем количество
отрезков, оно и будет ответом в задаче.
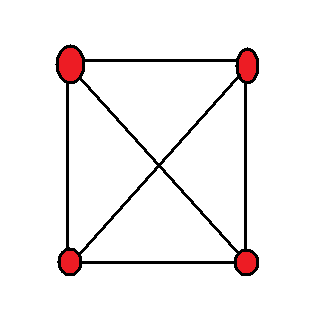
Ответ: шесть рукопожатий.





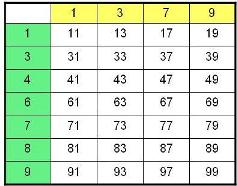
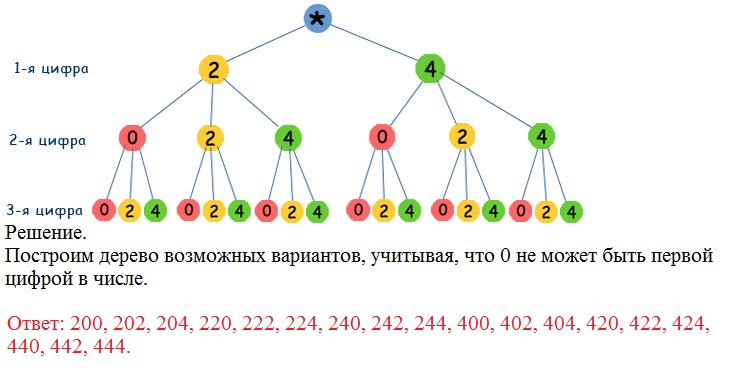
Составьте все возможные трехзначные числа из цифр 0, 2, 4?
 Онлайн ОЛИМПИАДА
Онлайн ОЛИМПИАДА
Ещё задания
Задача №1
Ленивая дочь из мультфильма «Двенадцать месяцев», лёжа на печи, посмотрела на потолок и насчитала некоторое количество мух. Но вот прилетели ещё 5 мух, потом улетели 7 мух, затем прилетели 2 мухи и ещё одна. Затем все 16 мух улетели. Сколько мух насчитала Ленивая дочь сначала? (3б)
Задача №2
Трое фермеров с сыновьями привезли на рынок свою продукцию. Им выделено на рынке три места. Фермеры решили расположиться на этих местах парами, чтобы каждый фермер вёл торговлю на двух рыночных точках. Чтобы определить оптимальные места для торговли парами, каждые двое из фермеров определили совместные массы привезенных продуктов. Получили такие результаты: 360 кг, 400 кг, 440 кг. Какова общая масса привезенных продуктов? (2б)
Задача №3
В кинотеатре, вмещающем 500 зрителей, трижды показали фильм, получивший приз на Каннском фестивале. Каждый раз зал был заполнен полностью. При этом 800 человек посмотрели фильм ровно по одному разу, 200 человек — ровно по два раза. Сколько человек посмотрели фильм три раза? (5б)
Задача №4
Нужно переложить одну спичку так, чтобы равенство стало верным. Нарисуй ответ. (2б)

Задача №5
Сосчитай треугольники (5б)

Задача №6
В некоторой фирме имеется директор фирмы, его заместитель, начальники трёх отделов, их заместители и рядовые сотрудники отделов. Известно, что тех, у кого есть начальник, в 5 раз больше, чем начальников. Сколько в фирме рядовых сотрудников, если рядовые сотрудники подчиняются директору, его заместителям, начальникам всех отделов и их заместителям? (8б)
Задача №7
Какой объём древесины использован для изготовления 100 упаковок по 10 коробков спичек в каждой, если каждая коробка содержит по 38 спичек, имеющих длину 5 см, ширину 2 мм и высоту 2 мм? Треть использованной древесины составляют отходы. Объем вырази в см3. (10б)
Задача №8.
Разгадай математический ребус (7б)
ВАГОН
+ ВАГОН
СОСТАВ
Задача №9
Квадратная клумба в парке засажена розами. Расстояние между кустами в ряду равно 80 см, а между рядами — 1 м 20 см. Сколько кустов роз на клумбе, если в каждом ряду 16 кустов?(3б)
Задача №10
Во дворе ходят курочки и козочки. У них вместе 44 ноги и 14 голов. Сколько курочек и козочек во дворе? (5б)
Решение олимпиадных заданий по математике для 4 класса
(областной уровень)
максимальное количество баллов – 50
Задача №1
Ленивая дочь из мультфильма «Двенадцать месяцев», лёжа на печи, посмотрела на потолок и насчитала некоторое количество мух. Но вот прилетели ещё 5 мух, потом улетели 7 мух, затем прилетели 2 мухи и ещё одна. Затем все 16 мух улетели. Сколько мух насчитала Ленивая дочь сначала? (3б)
Максимальное количество баллов - 3
Принимается любое решение. Если ход решения задачи верный, но допущена вычислительная ошибка, повлекшая за собой неточный ответ, то снимается 0,5 балла. За ошибки в наименовании или за отсутствие наименования снимается 0,5 балла. Если ученик дает только верный ответ, а какое – либо решение и пояснение к нему отсутствует, то он получает только 1 балл.
Решение:
1 способ:
1) 5+2+1=8 (шт.) – столько мух всего прилетело.
2) 8-7=1(шт.) – столько из прилетевших мух осталось.
3)16-1=15(шт.) – столько мух насчитала Ленивая дочь сначала.
2 способ: через составление уравнения
Х+5-7+2+1=16
Х+1=16
Х=16-1
Х=15
3 способ: через построение цепочки и выполнение обратных операций.
Х+5-7+2+1=16 выполняем обратные операции: 16-1-2+7-5=15
Ответ: 15 мух.
Задача №2
Трое фермеров с сыновьями привезли на рынок свою продукцию. Им выделено на рынке три места. Фермеры решили расположиться на этих местах парами, чтобы каждый фермер вёл торговлю на двух рыночных точках. Чтобы определить оптимальные места для торговли парами, каждые двое из фермеров определили совместные массы привезенных продуктов. Получили такие результаты: 360 кг, 400 кг, 440 кг. Какова общая масса привезенных продуктов? (2б)
Максимальное количество баллов - 2
Принимается любое верное решение. Каждый верный шаг оценивается в 1 балл. Должны быть пояснения к ним. Если ход решения задачи верный, но допущена вычислительная ошибка, повлекшая за собой неточный ответ, то снимается 0,5 балла. За ошибки в наименовании или за отсутствие наименования снимается 0,5 балла. Если ученик дает только верный ответ, а какое – либо решение и пояснение к нему отсутствует, то он получает только 1 балл.
Решение:
1)360+400+440=1200 (кг)- удвоенная масса привезенных продуктов
2) 1200:2=600(кг)
Объяснения: Массы 360 кг, 400 кг, 440 кг являются суммами масс продуктов соответственно первого и второго, первого и третьего, второго и третьего фермеров. Среди этих масс масса продукции каждого фермера встречается дважды. Их сумма 360 + 400 + 440 = 1200 (кг) равна удвоенной общей массе привезенных продуктов. Поэтому общая масса привезенных продуктов равна 600 кг.
Ответ: 600 кг.
Задача №3
В кинотеатре, вмещающем 500 зрителей, трижды показали фильм, получивший приз на Каннском фестивале. Каждый раз зал был заполнен полностью. При этом 800 человек посмотрели фильм ровно по одному разу, 200 человек — ровно по два раза. Сколько человек посмотрели фильм три раза? (5б)
Максимальное количество баллов - 5
Каждый верный шаг оценивается в 1 балл. Задача решается по действиям. Должны быть пояснения к ним. Если ход решения задачи верный, но допущена вычислительная ошибка, повлекшая за собой неточный ответ, то снимается 0,5 балла. За ошибки в наименовании или за отсутствие наименования снимается 0,5 балла. Если ученик дает только верный ответ, а какое – либо решение и пояснение к нему отсутствует, то он получает только 1 балл.
Решение
500⋅3 = 1500 (м.)- занято на трех просмотрах 200⋅2 = 400 (м.) - зрители, смотревшие фильм по два раза. 400+800= 1200(м.) – смотрели фильм по два раза и один раз 1500 – 1200 = 300 (м.)- смотревшие фильм по три раза. 300:3 = 100 (ч). Ответ: 100 человек
Задача №4
Нужно переложить одну спичку так, чтобы равенство стало верным. Нарисуй ответ. (2б)

Решение:
Максимальное количество баллов - 2

Задача №5
Сосчитай треугольники (5б)

Ответ: 15 треугольников
Максимальное количество баллов - 5
Если ребенок нашел 12-14 треугольников - 4 балла,
11-10 треугольников - 3 балла,
9-7 треугольников - 2 балла,
менее 7 - 1 балл
Задача №6
В некоторой фирме имеется директор фирмы, его заместитель, начальники трёх отделов, их заместители и рядовые сотрудники отделов. Известно, что тех, у кого есть начальник, в 5 раз больше, чем начальников. Сколько в фирме рядовых сотрудников, если рядовые сотрудники подчиняются директору, его заместителям, начальникам всех отделов и их заместителям? (8б)
Максимальное количество баллов - 8
Решение:
1) 1+1+3+3=8 (ч)- начальников в фирме
2) 8*5=40 (ч) - подчинённые
3) 8-1=7 или 1+3+3=7 (ч) - начальники, у которых есть начальники
4) 40-7=33 (ч)
Ответ. 33 рядовых сотрудника.
Каждый верный шаг оценивается в 2 балл.
Задача решается по действиям. Должны быть пояснения к ним. Если ход решения задачи верный, но допущена вычислительная ошибка, повлекшая за собой неточный ответ, то снимается 0,5 балла. За ошибки в наименовании или за отсутствие наименования снимается 0,5 балла. Если ученик дает только верный ответ, а какое – либо решение и пояснение к нему отсутствует, то он получает только 1 балл.
Задача №7
Какой объём древесины использован для изготовления 100 упаковок по 10 коробков спичек в каждой, если каждая коробка содержит по 38 спичек, имеющих длину 5 см, ширину 2 мм и высоту 2 мм? Треть использованной древесины составляют отходы. Объем вырази в см3. (10б)
Максимальное количество баллов - 10
Каждый верный шаг оценивается в 2 балла. Задача решается по действиям. Должны быть пояснения к ним. Если ход решения задачи верный, но допущена вычислительная ошибка, повлекшая за собой неточный ответ, то снимается 0,5 балла. За ошибки в наименовании или за отсутствие наименования снимается 0,5 балла. Если ученик дает только верный ответ, а какое – либо решение и пояснение к нему отсутствует, то он получает только 1 балл.
Решение:
1) 50⋅2⋅2 = 200 (мм3) - объём древесины в одной спичке
2) 10⋅100= 1000 ( кор.)- всего
2) 38⋅1000 = 38 000(сп.)- всего
3) 200⋅38 000 = 7 600 000 (мм3)- объём древесины в 38 000 спичек.
Это составляет две третьих всей использованной древесины.
4)7 600 000:2 ⋅3 = 11 400 000 мм3
11 400 000 мм3 = 11 400 см3.
Ответ. 11 400 см3.
Задача №8.
Разгадай математический ребус (7б)
ВАГОН
+ ВАГОН
СОСТАВ
Решение:
Максимальное количество баллов - 7. За каждую верную цифру 1балл.
ВАГОН+ВАГОН=СОСТАВ. Вы имеете два неизвестных пятизначных числа, сумма которых шестизначное число, значит В+В больше 10-ти и С равно 1. Замените символы С на 1.
Сумма А+А – однозначное или двухзначное число с единицей на конце, это возможно в том случае, если сумма Г+Г больше 10 и А равно либо 0, либо 5. Попробуйте предположить, что А равно 0, тогда О равно 5-ти, что не удовлетворяет условиям задачи, т. к. в этом случае В+В=2В не может равняться 15-ти. Следовательно, А=5. Замените все символы А на 5.
Сумма О+О=2О – четное число, может быть равна 5 или 15 лишь в том случае, если сумма Н+Н – двухзначное число, т. е. Н больше 6-ти. Если О+О=5, то О=2. Это решение неверно, т. к. В+В=2В+1, т. е. О должно быть число нечетное. Значит, О равно 7-ми. Замените все О на 7.
Легко заметить, что В равно 8-ми, тогда Н=9. Замените все буквы на найденные числовые значения.
Замените в примере оставшиеся буквы на числа: Г=6 и Т=3.
Ответ: 85679+85679=171358.
Задача №9
Квадратная клумба в парке засажена розами. Расстояние между кустами в ряду равно 80 см, а между рядами — 1 м 20 см. Сколько кустов роз на клумбе, если в каждом ряду 16 кустов?(3б)
Максимальное количество баллов - 3
Каждый верный шаг оценивается в 1 балл. Задача решается по действиям. Должны быть пояснения к ним. Если ход решения задачи верный, но допущена вычислительная ошибка, повлекшая за собой неточный ответ, то снимается 0,5 балла. За ошибки в наименовании или за отсутствие наименования снимается 0,5 балла. Если ученик дает только верный ответ, а какое – либо решение и пояснение к нему отсутствует, то он получает только 1 балл.
Решение:
1) 80⋅15 = 1200 см. - сторона клумбы
2) 1200:120 = 10 (р) - на клумбе
3) 16*10=160 (роз)
Ответ: на клумбе 160 роз
Задача №10
Во дворе ходят курочки и козочки. У них вместе 44 ноги и 14 голов. Сколько курочек и козочек во дворе?
Максимальное количество баллов - 5
Принимается любое решение. Каждый верный шаг оценивается в 1 балл. Если ход решения задачи верный, но допущена вычислительная ошибка, повлекшая за собой неточный ответ, то снимается 0,5 балла. За ошибки в наименовании или за отсутствие наименования снимается 0,5 балла. Если ученик дает только верный ответ, а какое – либо решение и пояснение к нему отсутствует, то он получает только 1 балл.
1 способ: уравнением
Количество козочек обозначим "Х", количество курочек обозначим "У".
Составим уравнение: Х + У = 14
Второе уравнение: 4Х + 2У = 44
Из первого уравнения следует, что У = 14 - Х
Подставим этот У во второе уравнение: 4Х + 2(14 - Х) = 44
Раскроем скобки: 4Х + 28 - 2Х = 44
Перенесем 28 в правую часть уравнения: 4Х - 2Х = 44 - 28
Следовательно, получается, что 2Х = 16. Х = 8, т. е. коз 8.
14 - 8 = 6. У = 6, т. е. кур 6.
2 способ: по действиям
Всего их 14 животных. У кур по 2 ноги, у коз по 4 ноги.
1) 14*2=28 (н)- Если бы были только куры
2) 44 - 28 = 16 (н)- принадлежат козам
3) 16:2 = 8 козочек
4) 14 - 8 = 6 курочек.
3 способ: методом подбора 4*8+2*6=44
Ответ: 8 козочек и 6 курочек
еще задачки
Мама купила Оле, Саше и Паше по — мороженому: пломбир, шоколадное и клубничное. Оля ест не клубничное и не пломбир. Саша не пломбир и не шоколадное, Паша не любит шоколад и клубничное мороженое. Какое мороженое ест каждый ребенок?
Начертим таблицу и заполним ее данными. Чертим таблицу 4х3. Не подходящее по условию значение обозначим <<->> , подходящее <<+>>.

Так как Оля ест не клубничное и не пломбир, в эти графы ставим минус. Получается, что для Оли подходит шоколадное, там ставим плюс. Саша ест не пломбир и не шоколадное, ставим там минус. Для нее подходящее значение клубничное. Так как Паша не любит шоколад, то и мороженное шоколадное он есть не будет, ставим минус, и на клубничное тоже. Паша ест пломбир.
Ответ: Оля-шоколадное, Саша-клубничное, Паша-пломбир.
Текстовые задачи типа <<Считаем ноги и головы>> очень популярны в математических олимпиадах и в заданиях со звездочкой в учебнике.
На ферме живут гуси и овцы. В сумме у них 40 голов и 94 ноги. Сколько на ферме проживает гусей? и сколько овец?

Разберемся для начала со всеми ногами. Мы знаем, что у овцы их четыре, а гуся две. Давайте посчитаем так, если у всех по две ноги. Так как голов 40, то получается:
40 • 2 = 80 ног.
По условию в задаче всего 94 ноги, найдем так называемые <<лишние>> ноги:
94 — 80 = 14.
Если эти 14 ног лишние, значит они принадлежат четвероногим овцам, и теперь мы сможем определить количество овец:
14 : 2 = 7 овец.
Теперь осталось вычислить сколько на ферме гусей. Для этого просто вычтем из общего числа голов те, которые принадлежат овцам:
40 — 7 = 33 гуся.
Ответ: 7 овец и 33 гуся.
Еще одна не менее популярная задача на <<рукопожатия>>.
Ваня на детской площадке встретил своих друзей Петю, Машу и Колю. При встрече они все обменялись рукопожатиями. Сколько всего было рукопожатий при встрече?

Ответ: шесть рукопожатий.






Составьте все возможные трехзначные числа из цифр 0, 2, 4?
 Онлайн ОЛИМПИАДА
Онлайн ОЛИМПИАДА Ещё задания
Задача №1
Ленивая дочь из мультфильма «Двенадцать месяцев», лёжа на печи, посмотрела на потолок и насчитала некоторое количество мух. Но вот прилетели ещё 5 мух, потом улетели 7 мух, затем прилетели 2 мухи и ещё одна. Затем все 16 мух улетели. Сколько мух насчитала Ленивая дочь сначала? (3б)
Задача №2
Трое фермеров с сыновьями привезли на рынок свою продукцию. Им выделено на рынке три места. Фермеры решили расположиться на этих местах парами, чтобы каждый фермер вёл торговлю на двух рыночных точках. Чтобы определить оптимальные места для торговли парами, каждые двое из фермеров определили совместные массы привезенных продуктов. Получили такие результаты: 360 кг, 400 кг, 440 кг. Какова общая масса привезенных продуктов? (2б)
Задача №3
В кинотеатре, вмещающем 500 зрителей, трижды показали фильм, получивший приз на Каннском фестивале. Каждый раз зал был заполнен полностью. При этом 800 человек посмотрели фильм ровно по одному разу, 200 человек — ровно по два раза. Сколько человек посмотрели фильм три раза? (5б)
Задача №4
Нужно переложить одну спичку так, чтобы равенство стало верным. Нарисуй ответ. (2б)

Задача №5
Сосчитай треугольники (5б)

Задача №6
В некоторой фирме имеется директор фирмы, его заместитель, начальники трёх отделов, их заместители и рядовые сотрудники отделов. Известно, что тех, у кого есть начальник, в 5 раз больше, чем начальников. Сколько в фирме рядовых сотрудников, если рядовые сотрудники подчиняются директору, его заместителям, начальникам всех отделов и их заместителям? (8б)
Задача №7
Какой объём древесины использован для изготовления 100 упаковок по 10 коробков спичек в каждой, если каждая коробка содержит по 38 спичек, имеющих длину 5 см, ширину 2 мм и высоту 2 мм? Треть использованной древесины составляют отходы. Объем вырази в см3. (10б)
Задача №8.
Разгадай математический ребус (7б)
ВАГОН
+ ВАГОН
СОСТАВ
Задача №9
Квадратная клумба в парке засажена розами. Расстояние между кустами в ряду равно 80 см, а между рядами — 1 м 20 см. Сколько кустов роз на клумбе, если в каждом ряду 16 кустов?(3б)
Задача №10
Во дворе ходят курочки и козочки. У них вместе 44 ноги и 14 голов. Сколько курочек и козочек во дворе? (5б)
Решение олимпиадных заданий по математике для 4 класса
(областной уровень)
максимальное количество баллов – 50
Задача №1
Ленивая дочь из мультфильма «Двенадцать месяцев», лёжа на печи, посмотрела на потолок и насчитала некоторое количество мух. Но вот прилетели ещё 5 мух, потом улетели 7 мух, затем прилетели 2 мухи и ещё одна. Затем все 16 мух улетели. Сколько мух насчитала Ленивая дочь сначала? (3б)
Максимальное количество баллов - 3
Принимается любое решение. Если ход решения задачи верный, но допущена вычислительная ошибка, повлекшая за собой неточный ответ, то снимается 0,5 балла. За ошибки в наименовании или за отсутствие наименования снимается 0,5 балла. Если ученик дает только верный ответ, а какое – либо решение и пояснение к нему отсутствует, то он получает только 1 балл.
Решение:
1 способ:
1) 5+2+1=8 (шт.) – столько мух всего прилетело.
2) 8-7=1(шт.) – столько из прилетевших мух осталось.
3)16-1=15(шт.) – столько мух насчитала Ленивая дочь сначала.
2 способ: через составление уравнения
Х+5-7+2+1=16
Х+1=16
Х=16-1
Х=15
3 способ: через построение цепочки и выполнение обратных операций.
Х+5-7+2+1=16 выполняем обратные операции: 16-1-2+7-5=15
Ответ: 15 мух.
Задача №2
Трое фермеров с сыновьями привезли на рынок свою продукцию. Им выделено на рынке три места. Фермеры решили расположиться на этих местах парами, чтобы каждый фермер вёл торговлю на двух рыночных точках. Чтобы определить оптимальные места для торговли парами, каждые двое из фермеров определили совместные массы привезенных продуктов. Получили такие результаты: 360 кг, 400 кг, 440 кг. Какова общая масса привезенных продуктов? (2б)
Максимальное количество баллов - 2
Принимается любое верное решение. Каждый верный шаг оценивается в 1 балл. Должны быть пояснения к ним. Если ход решения задачи верный, но допущена вычислительная ошибка, повлекшая за собой неточный ответ, то снимается 0,5 балла. За ошибки в наименовании или за отсутствие наименования снимается 0,5 балла. Если ученик дает только верный ответ, а какое – либо решение и пояснение к нему отсутствует, то он получает только 1 балл.
Решение:
1)360+400+440=1200 (кг)- удвоенная масса привезенных продуктов
2) 1200:2=600(кг)
Объяснения: Массы 360 кг, 400 кг, 440 кг являются суммами масс продуктов соответственно первого и второго, первого и третьего, второго и третьего фермеров. Среди этих масс масса продукции каждого фермера встречается дважды. Их сумма 360 + 400 + 440 = 1200 (кг) равна удвоенной общей массе привезенных продуктов. Поэтому общая масса привезенных продуктов равна 600 кг.
Ответ: 600 кг.
Задача №3
В кинотеатре, вмещающем 500 зрителей, трижды показали фильм, получивший приз на Каннском фестивале. Каждый раз зал был заполнен полностью. При этом 800 человек посмотрели фильм ровно по одному разу, 200 человек — ровно по два раза. Сколько человек посмотрели фильм три раза? (5б)
Максимальное количество баллов - 5
Каждый верный шаг оценивается в 1 балл. Задача решается по действиям. Должны быть пояснения к ним. Если ход решения задачи верный, но допущена вычислительная ошибка, повлекшая за собой неточный ответ, то снимается 0,5 балла. За ошибки в наименовании или за отсутствие наименования снимается 0,5 балла. Если ученик дает только верный ответ, а какое – либо решение и пояснение к нему отсутствует, то он получает только 1 балл.
Решение
500⋅3 = 1500 (м.)- занято на трех просмотрах 200⋅2 = 400 (м.) - зрители, смотревшие фильм по два раза. 400+800= 1200(м.) – смотрели фильм по два раза и один раз 1500 – 1200 = 300 (м.)- смотревшие фильм по три раза. 300:3 = 100 (ч). Ответ: 100 человек
Задача №4
Нужно переложить одну спичку так, чтобы равенство стало верным. Нарисуй ответ. (2б)

Решение:
Максимальное количество баллов - 2

Задача №5
Сосчитай треугольники (5б)

Ответ: 15 треугольников
Максимальное количество баллов - 5
Если ребенок нашел 12-14 треугольников - 4 балла,
11-10 треугольников - 3 балла,
9-7 треугольников - 2 балла,
менее 7 - 1 балл
Задача №6
В некоторой фирме имеется директор фирмы, его заместитель, начальники трёх отделов, их заместители и рядовые сотрудники отделов. Известно, что тех, у кого есть начальник, в 5 раз больше, чем начальников. Сколько в фирме рядовых сотрудников, если рядовые сотрудники подчиняются директору, его заместителям, начальникам всех отделов и их заместителям? (8б)
Максимальное количество баллов - 8
Решение:
1) 1+1+3+3=8 (ч)- начальников в фирме
2) 8*5=40 (ч) - подчинённые
3) 8-1=7 или 1+3+3=7 (ч) - начальники, у которых есть начальники
4) 40-7=33 (ч)
Ответ. 33 рядовых сотрудника.
Каждый верный шаг оценивается в 2 балл.
Задача решается по действиям. Должны быть пояснения к ним. Если ход решения задачи верный, но допущена вычислительная ошибка, повлекшая за собой неточный ответ, то снимается 0,5 балла. За ошибки в наименовании или за отсутствие наименования снимается 0,5 балла. Если ученик дает только верный ответ, а какое – либо решение и пояснение к нему отсутствует, то он получает только 1 балл.
Задача №7
Какой объём древесины использован для изготовления 100 упаковок по 10 коробков спичек в каждой, если каждая коробка содержит по 38 спичек, имеющих длину 5 см, ширину 2 мм и высоту 2 мм? Треть использованной древесины составляют отходы. Объем вырази в см3. (10б)
Максимальное количество баллов - 10
Каждый верный шаг оценивается в 2 балла. Задача решается по действиям. Должны быть пояснения к ним. Если ход решения задачи верный, но допущена вычислительная ошибка, повлекшая за собой неточный ответ, то снимается 0,5 балла. За ошибки в наименовании или за отсутствие наименования снимается 0,5 балла. Если ученик дает только верный ответ, а какое – либо решение и пояснение к нему отсутствует, то он получает только 1 балл.
Решение:
1) 50⋅2⋅2 = 200 (мм3) - объём древесины в одной спичке
2) 10⋅100= 1000 ( кор.)- всего
2) 38⋅1000 = 38 000(сп.)- всего
3) 200⋅38 000 = 7 600 000 (мм3)- объём древесины в 38 000 спичек.
Это составляет две третьих всей использованной древесины.
4)7 600 000:2 ⋅3 = 11 400 000 мм3
11 400 000 мм3 = 11 400 см3.
Ответ. 11 400 см3.
Задача №8.
Разгадай математический ребус (7б)
ВАГОН
+ ВАГОН
СОСТАВ
Решение:
Максимальное количество баллов - 7. За каждую верную цифру 1балл.
ВАГОН+ВАГОН=СОСТАВ. Вы имеете два неизвестных пятизначных числа, сумма которых шестизначное число, значит В+В больше 10-ти и С равно 1. Замените символы С на 1.
Сумма А+А – однозначное или двухзначное число с единицей на конце, это возможно в том случае, если сумма Г+Г больше 10 и А равно либо 0, либо 5. Попробуйте предположить, что А равно 0, тогда О равно 5-ти, что не удовлетворяет условиям задачи, т. к. в этом случае В+В=2В не может равняться 15-ти. Следовательно, А=5. Замените все символы А на 5.
Сумма О+О=2О – четное число, может быть равна 5 или 15 лишь в том случае, если сумма Н+Н – двухзначное число, т. е. Н больше 6-ти. Если О+О=5, то О=2. Это решение неверно, т. к. В+В=2В+1, т. е. О должно быть число нечетное. Значит, О равно 7-ми. Замените все О на 7.
Легко заметить, что В равно 8-ми, тогда Н=9. Замените все буквы на найденные числовые значения.
Замените в примере оставшиеся буквы на числа: Г=6 и Т=3.
Ответ: 85679+85679=171358.
Задача №9
Квадратная клумба в парке засажена розами. Расстояние между кустами в ряду равно 80 см, а между рядами — 1 м 20 см. Сколько кустов роз на клумбе, если в каждом ряду 16 кустов?(3б)
Максимальное количество баллов - 3
Каждый верный шаг оценивается в 1 балл. Задача решается по действиям. Должны быть пояснения к ним. Если ход решения задачи верный, но допущена вычислительная ошибка, повлекшая за собой неточный ответ, то снимается 0,5 балла. За ошибки в наименовании или за отсутствие наименования снимается 0,5 балла. Если ученик дает только верный ответ, а какое – либо решение и пояснение к нему отсутствует, то он получает только 1 балл.
Решение:
1) 80⋅15 = 1200 см. - сторона клумбы
2) 1200:120 = 10 (р) - на клумбе
3) 16*10=160 (роз)
Ответ: на клумбе 160 роз
Задача №10
Во дворе ходят курочки и козочки. У них вместе 44 ноги и 14 голов. Сколько курочек и козочек во дворе?
Максимальное количество баллов - 5
Принимается любое решение. Каждый верный шаг оценивается в 1 балл. Если ход решения задачи верный, но допущена вычислительная ошибка, повлекшая за собой неточный ответ, то снимается 0,5 балла. За ошибки в наименовании или за отсутствие наименования снимается 0,5 балла. Если ученик дает только верный ответ, а какое – либо решение и пояснение к нему отсутствует, то он получает только 1 балл.
1 способ: уравнением
Количество козочек обозначим "Х", количество курочек обозначим "У".
Составим уравнение: Х + У = 14
Второе уравнение: 4Х + 2У = 44
Из первого уравнения следует, что У = 14 - Х
Подставим этот У во второе уравнение: 4Х + 2(14 - Х) = 44
Раскроем скобки: 4Х + 28 - 2Х = 44
Перенесем 28 в правую часть уравнения: 4Х - 2Х = 44 - 28
Следовательно, получается, что 2Х = 16. Х = 8, т. е. коз 8.
14 - 8 = 6. У = 6, т. е. кур 6.
2 способ: по действиям
Всего их 14 животных. У кур по 2 ноги, у коз по 4 ноги.
1) 14*2=28 (н)- Если бы были только куры
2) 44 - 28 = 16 (н)- принадлежат козам
3) 16:2 = 8 козочек
4) 14 - 8 = 6 курочек.
3 способ: методом подбора 4*8+2*6=44
Ответ: 8 козочек и 6 курочек
еще задачки
Задание 1.
Поменяйте местами две цифры, чтобы получилось верное равенство:
2012= 1719 + 275
Задание 2.
Петя задумал два числа так, что одно из них в 3 раза больше другого, а сумма их равна 68. Какие числа задумал Петя?
Задание 3.
Чему равны стороны прямоугольника, площадь которого равна 12 см2, а периметр равен 26 см?
Задание 4.
Используя пять «двоек» составьте выражение, значение которого равно:
а)18;
б) 1;
в) 113;
г) 26.
Задание 5.
На уроке физкультуры мальчики построились в шеренгу. Потом между каждыми двумя мальчиками встала девочка. Всего в шеренге оказалось 25 детей. Сколько мальчиков стояло в шеренге?
Задание 6.
Ребята Саша, Женя, Коля и Миша отправились в поход. У каждого из них был рюкзак. У Саши рюкзак был легче, чем у Коли, но тяжелее, чем у Жени. У Миши рюкзак легче, чем у Коли, но тяжелее, чем у Саши. Ребята идут друг за другом. Каждый впереди идущий имеет более лёгкий рюкзак. В каком порядке идут ребята?
Задание 7.
Теплоход уходит в плавание во вторник в полдень. Плавание продлится 100 часов. Каков день недели и час его прибытия?
Задание 8.
Когда ваши родители были детьми, молоко продавали в литровых и пол-литровых стеклянных бутылках. Пустые бутылки из-под молока можно было сдавать в магазин по цене 20 коп. и 15 коп. соответственно. Коля пошёл в магазин без денег, взяв с собой пустые бутылки – 6 литровых и 6 пол-литровых. В магазине было разливное молоко по 22 коп. за литр. Коля решил сдать часть бутылок, а купленное на полученные деньги молоко налить в оставшиеся бутылки. Какое наибольшее количество молока он сможет принести домой?
Задание 9.
Если сторону квадрата, периметр которого 36 см, уменьшить в 3 раза, то получится ширина прямоугольника, периметр которого 22 см. Найдите длину этого прямоугольника и вычислите его площадь.
Задание 10.
Шестеро тянут репку: дедка вдвое сильнее бабки, бабка вдвое сильнее внучки, внучка вдвое сильнее Жучки, Жучка вдвое сильнее кошки, кошка вдвое сильнее мышки. Сколько нужно позвать мышек, чтобы они сами вытянули репку?
Задание 11.
Вставьте цифры вместо букв а и в, чтобы получились верные результаты.
Задание 12.
Муравьишка ехал на гусенице 24 минуты, а потом пересел на жука и проехал в 4 раза больший путь. Сколько минут он ехал на жуке, если жук передвигается в 8 раз быстрее гусеницы?
Задание 13.
Реши пример по действиям:
60000 : (975 + 29535 - 84 - 426) · 8 · 19=
Задание 14.
Квадратный участок земли (длина стороны квадрата 40 м) состоит из 16 квадратных грядок. Для орошения участка между некоторыми грядками надо проложить трубу из места, показанного точкой. Эта труба длиной 100 м должна разделить участок на 2 равные части. Покажи, как надо проложить трубу? Если сможешь, покажи не один вариант решения.
Задание 15.
В полдень от пристани отошёл пароход со скоростью 16 км/ч. Через 3 часа от той же пристани в том же направлении отошёл теплоход, который через 12 часов после своего выхода догнал пароход. Определи скорость теплохода.
Ответы (максимум - 44 балла)
Задание 1. Продолжи ряд, сохраняя закономерность:
а) 25, 4, 100, 26, 5, 130, _____, _____, _____.
б) 16, 48, 17, 51, 18, 54, _____, _____ .
в) 8, 15, 16, 30, 32, 60, 64, 120, _____, ______.
Задание 2. Мама приготовила школьную форму для Димы. Сколько разных костюмов может составить Дима, если у него три рубашки, двое брюк и два галстука, и все эти предметы подходят друг другу?
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 3. Костя начал делать уроки в 16 часов 10 минут, через 1 час 55 минут к нему пришли Андрей и Никита и пригласили его погулять. Сколько времени Костя может потратить на прогулку, если ему необходимо закончить приготовление уроков в 8 часов вечера, а ещё осталось сделать математику, на которую он потратит 45 минут. Напиши решение задачи и ответ, сделай необходимые пояснения.
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 4. В таблице для некоторых продуктов указано, сколько граммов этих продуктов содержится в чайной и столовой ложке. Эти данные могут пригодиться при приготовлении пищи.
Используя эту таблицу, ответь на вопросы:
1.Сколько граммов сахара содержится в одной чайной ложке?
Ответ:___________
2.Как с помощью ложек отмерить продукты для приготовления одной порции манной каши, если для неё надо 45г манной крупы, 5г сливочного масла и 5г сахара?
Ответ: ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 5. Кролик даёт в год 400 г пуха. Для его содержания нужна клетка длиной 75 см и шириной 60 см. Какую площадь нужно отвести под клетки для кроликов, с которых за год получают 24 кг пуха? ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 6. Из металлической заготовки вытачивают деталь. Стружки, которые получились при вытачивании 8 деталей, можно переплавить в одну заготовку. Сколько деталей можно сделать из 64 заготовок?
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 7. В таблице представлены массы некоторых животных.
Ира начала изображать массы животных в виде пиктограммы.
Условное обозначение: = 400 кг
Сколько условных обозначений нужно нарисовать в последней строке, чтобы получилась правильная пиктограмма? Запиши в таблицу количество условных обозначений каждого вида.
Задание 8. Марине для приготовления кекса по рецепту необходимо использовать 100 мл молока. На рисунке изображён сосуд для измерения объёма жидкости, в котором налито молоко. Объём измеряется в миллилитрах – мл. Сколько ещё молока необходимо долить в сосуд Марине, чтобы не нарушить рецепт?
Решение: ________________________________________________________________________________________________________________________________________________________________________________________________________________
Ответ: ____________________________________________
Задание 9. Расставь порядок действий. Найдите значение выражений.
450 : ( 30 х 3 ) х 60 – 94 х 3 + 68 : ( 51 : 3) =
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
______________________________________________________________________________________________________________________________________________________________________________________________________
Всероссийская олимпиада школьников по математике
Муниципальный этап. Ответы
4 класс (2019-2020 учебный год)
Комментариев нет:
Отправить комментарий